Los autómatas celulares aparecen por primera vez a finales de los años 40, más concretamente a partir de 1947, de la mano de Von Neumann y Stanislaw Ulam, dos expertos en física computacional con una fuerte relación de amistad tras las colaboraciones que realizaron durante el desarrollo del proyecto Manhattan. El origen de la idea proviene del desarrollo de unos estudios que Von Neumann realizó sobre sistemas con componentes no confiables (es decir, computación que tolerase fallos) poco después de terminar el proyecto EDVAC1. Von Neumann comenzó estudiando el desarrollo de autómatas auto-reproductivos basándose en ecuaciones diferenciales parciales, pero desechó este método porque no fue capaz de encontrar reglas explícitas y claras para poder llevar a la práctica estos autómatas. Sin embargo, Arthur W. Burks2 confirma que Stanislaw Ulam sugirió a John Von Neumann el uso de componentes celulares para desarrollar sus autómatas auto-reproductivos, lo cual llevó a una solución del problema de Von Neumann. El estudio no fue concluido, debido a la prematura muerte del cientifico en 1957.

Aunque la idea fue concebida, como decimos, a partir del año 1947, no sería hasta el año 1966 cuando se publicará en "Theory of Self-reproducing Automata”, libro de Von Neumann a título póstumo, completado y estructurado por el citado Arthur W. Burks. La intención de Von Neumann era principalmente desarrollar una máquina que pudiera construir a partir de sí misma otras máquinas y soportar comportamiento complejo. Finalmente, implementó la teoría de autómatas celulares en un vector de dos dimensiones en un dominio de enteros (ℤ x ℤ).

Poco después, en 1967, Konrad Zuse enunció su tesis, que se basa en la idea de que “El universo es un autómata celular”. En general, esta tesis enuncia que el Universo es un dispositivo computacional que se puede considerar como una gran máquina de computación, es decir, un autómata celular. Sería Edward Fredkin quien popularizase y extendiese está idea años más tarde basandose en el trabajo de Zuse, de ahí que a esta teoria se le llame “tesis de Zuse-Fredkin”.

Los trabajos de Von Neumann y Ulam, y de Zuse y Fredkin, precedieron a la divulgación realizada por Martin Gardner. Éste fue un conocido periodista dedicado a la divulgación científica y concretamente, matemática. Además de sus libros, desde 1956 y 1986 publicó una columna mensual en la revista Scientific American titulada Mathematical Games. En esta columna, Gardner publicó en octubre de 1970 un artículo sobre el Juego de la vida (Life), diseñado por John Conway, un matemático británico. Este juego es un autómata celular, que formalmente es equivalente a una máquina universal de Turing, o lo que es lo mismo, “todo lo que se puede computar algorítmicamente se puede computar en el juego de la vida”. Durante los años 70 y principios de los años 80, el juego de la vida tuvo un gran seguimiento de los aficionados de la época, llegando a crearse múltiples variantes del Juego de la vida.

Más recientemente, la figura de Stephen Wolfram es indispensable en el campo de los autómatas celulares. Este físico y matemático londinense, considerado desde pequeño como niño prodigio y experto en física de partículas, estudio entre 1983 y 1986 en el Instituto de estudios avanzados de Princeton donde se dedicó al estudio y simulación de autómatas celulares. Entre 1992 y 2002, Stephen Wolfram trabajó en su libro “A new kind of Science”3, donde hace un estudio extenso de los autómatas celulares y su aplicación en campos de simulación y estudio de la realidad, es decir, introduce la idea de que se puede modelar y entender cualquier fenómeno natural. Wolfram, que además es el creador del famoso software matemático “Mathematica”, clasificó el comportamiento de los autómatas celulares en clases y motivó varios avances en el campo de los autómatas celulares.

Anteriormente hemos descrito los avances más importantes referentes a los autómatas celulares, pero sin embargo, se nos quedan en el tintero algunas aportaciones a su estudio. A continuación se enumeran los estudios cientificos, computacionales y matematicos relacionados con los autómatas celulares.

• 1947 – 1957: John Von Neumann, con la colaboración de Stanislaw Ulam.
• 1966: Arthur W. Burks, terminación y publicación del libro Theory of Self-reproducing Automata, a nombre de Von Neumann.
• 1967: Konrad Zuse enuncia su tesis planteando que el Universo es un gran automata celular, siendo Edward Fredkin quien años más tarde popularizase el planteamiento.
• 1967: Ulam y Robert Schrandt investigaron automatas celulares de dos estados, incluso estudiaron automatas celulares en tres dimensiones.
• 1967 en adelante: Edgar Frank Codd plantea una variación del automata de Von Neumann variando el número de estados posibles para cada celula.
• 1960 – 1969: Gustav A. Hedlund realiza un estudio matematico teorico sobre los automatas, que culmina con la publicación de Endomorphisms and automorphisms of the shift dynamical system, Mathematical Systems Theory en 1969.
• 1970: John Conway crea el Juego de la Vida, el automata celular más representativo. Publicado por Martin Gardner en la revista Scientifist American.
• 1980 - 1990: Stephen Wolfram, investigación en profundidad de los autómatas celulares y su clasificación.
• 1980 - 2000: Carter Bays, estudio de formaciones tridimensionales a partir de automatas celulares.

A partir de los estudios de Von Neumann, un autómata celular es un modelo matemático para un sistema dinámico que evoluciona en pasos discretos. Es decir, es un modelo matemático para sistemas que soportan cambios; además, estos cambios se suceden cada tiempos constantes, razón por la cual, se usa una escala de enteros.

Para poder definir un autómata celular, debemos comenzar por decir que matemáticamente no existe una definición formal aceptada. Sin embargo, comúnmente se define mediante la descripción de una serie de elementos que componen el autómata celular.

Definimos, por tanto, una cuadrícula de dimensión n, también llamada lattice. Una lattice es uno de los nombres que se dan a los retículos, que son conjuntos de elementos parcialmente ordenados en los cuales todo subconjunto finito no vacio tiene supremo e ínfimo. Cada una de las celdas de la cuadricula (o elemento de la lattice) es una célula. En teoría, esta cuadricula se extiende como un retículo infinito de enteros, sin embargo, esto es imposible a la hora de implementarlo y aplicarlo a casos prácticos.

Cada una de estas celdas tomará un valor de un conjunto finito de estados k. Sin embargo, el estado de una célula no es lo único que afecta a su evolución, sino que el desarrollo de cada una depende de sí misma y de su entorno. Dependiendo del autómata y de sus condiciones, existirán un conjunto de estados y le afectaran de un modo u otro. Este concepto de vecindad, fue definido por Von Neumann.

En definitiva, el funcionamiento del autómata celular se basa en el uso de una función de transición, que se aplica a todas y cada una de las células de la cuadricula en cada paso de la evolución del sistema dinámico. Esta función toma los valores de cada cuadricula y las de su vecindad y elabora a partir de estos argumentos el valor nuevo para la cuadricula en cuestión.

Como hemos visto antes, los autómatas celulares son en teoría retículos compuestos de infinitos números enteros, lo cual es un problema a la hora de realizar aplicaciones prácticas de los autómatas celulares. Por eso, para dar cabida a los supuestos prácticos, debemos modificar la concepción teórica para dar cabida a retículos finitos. Esto nos obliga a concebir las condiciones de frontera: las funciones de transición realizan modificaciones en una célula basándose en el estado de dicha célula y en las de su vecindad, pero si dicha célula se encuentra en el borde, su vecindad queda reducida. ¿Qué hacer en estos casos? Se plantean varias opciones de actuación que la función de transición podrá considerar: podemos considerar una frontera abierta, en la que se considera la existencia de células fuera de la cuadricula con valores fijos (todas las celulas externas tienen el mismo estado); una segunda opción es usar una frontera reflectora, que usa los valores del borde de la matriz para las celulas exteriores; la tercera opción consiste en usar una frontera periódica, que se trata de considerar el sistema como una cuadricula enroyada, haciendo que el conjunto de celdas sea continuo; y por ultimo, existen la posibilidad de que el sistema no tenga frontera, haciendo que la cuadricula crezca en función de las necesidades del autómata.

En una escala lógica, el autómata celular unidimensional es el primer paso para entender la dinámica de los autómatas celulares. Consiste en una sola fila de células a los que se aplica un principio de vecindad básico de dos vecinos por célula y a los que igualmente se pueden aplicar las diversas condiciones de frontera que hemos nombrado anteriormente.

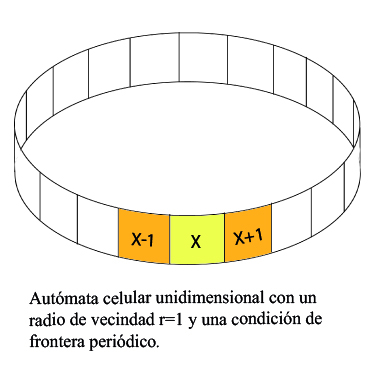
Como ejemplo, podemos tomar un autómata celular unidimensional con un radio de vecindad r=1, dos estados (0 y 1) y una condicion de frontera de tipo periódico, como el que se muestra en la imagen. Usaremos para este caso un tamaño de diez células y unas funciones de transición basadas en lo siguiente:

• Si ambos vecinos de la célula tienen el mismo estado, el estado de la célula a la que se aplica la funcion cambiará.
• Si ambos vecinos de la célula tienen distinto estado, el estado de la célula a la que se aplica se mantendrá igual.

Planteamos por tanto unos valores iniciales: 0001010011.

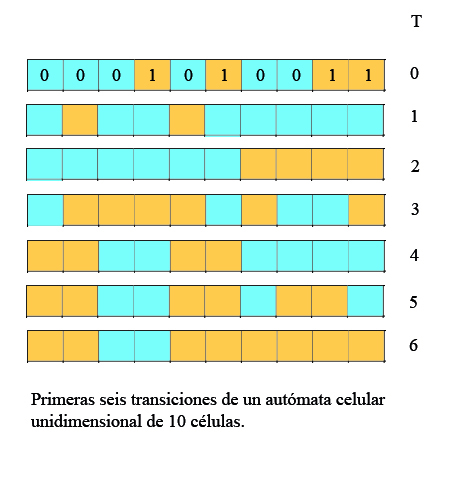
Stephen Wolfram clasificó el comportamiento de los automatas celulares unidimensionales. Según Wolfram, todo automata celular pertenece a una de las siguientes clases:

• Clase I. La evolución lleva a una configuración estable y homogénea, es decir, todas las células terminan por llegar al mismo valor.
• Clase II. La evolución lleva a un conjunto de estructuras simples que son estables o periódicas.
• Clase III. La evolución lleva a un patrón caótico1.
• Clase IV. La evolución lleva a estructuras aisladas que muestran un comportamiento complejo (es decir, ni completamente caótico, ni completamente ordenado, sino en la línea entre uno y otro, este suele ser el tipo de comportamiento más interesante que un sistema dinámico puede presentar).

Es el más común de los autómatas celulares a nivel de simulación y estudio. Consiste en la consabida cuadrícula compuesta por celulas (ℤ x ℤ), implantada por Von Neumann por consejo y Stanislaw Ulam. Este tipo de autómata celular, por ser el más estudiado, ha sido variado en múltiples ocasiones.

Ya hemos hablado del principio de vecindad de Von Neumann, que implicaba cuatro vecinos para cada célula, pero este no es el único. En 1970 se dio a conocer el juego de la vida de John Conway, que se basada en un principio de vecindad diferente. Este principio se conoce con el nombre de vecindad de Moore, y aplica ocho vecinos a cada célula, es decir, los cuatro que consideraba Von Neumann más las cuatro células de las diagonales respectivas. Además, se basaba en una condición de frontera de tipo periódico y dos estados posibles. Este juego de la vida consideraba tres reglas fundamentales para su funcionamiento:

1. Nacimiento: se reemplaza una célula muerta por una viva si dicha célula tiene exactamente 3 vecinos vivos.
2. Muerte: se reemplaza una célula viva por una muerta si dicha célula no tiene más de 1 vecino vivo (muerte por aislamiento) o si tiene más de 3 vecinos vivos (muerte por sobrepoblación).
3. Supervivencia: una célula viva permanecerá en ese estado si tiene 2 o 3 vecinos vivos.

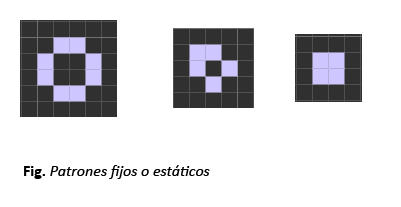
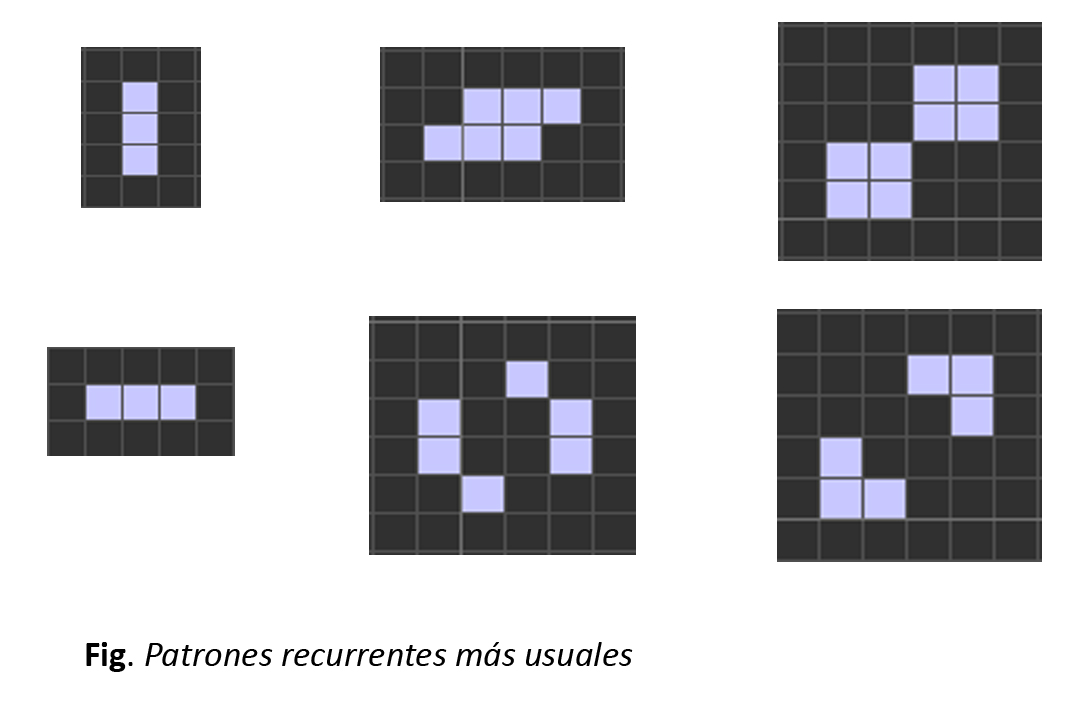
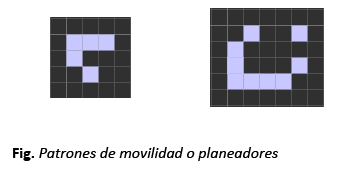
Producto del amplio estudio que han realizado múltiples expertos y estudiantes, se han descubierto y catalogado una serie de patrones característicos. Se diferencian entonces cuatro tipos de patrones: estáticos, patrones que no varían; recurrentes, patrones que varian de una posición a otra indefinidamente; patrones con movilidad, que se reproducen y se mueven por toda la cuadricula; matusalenes, que son patrones que tardan muchos pasos en estabilizarse.

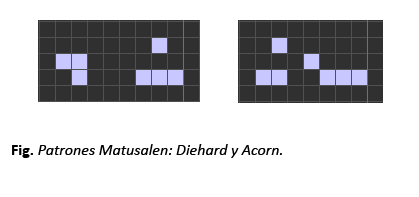
Especial atención merecen estos últimos, los matusalenes. Son una serie interesante de patrones que evolucionan durante varias generaciones antes de estabilizarse. Diehard es uno de estos patrones, que se estabiliza tras 130 turnos, desapareciendo, mientras que Acorn llega a 5206 transiciones antes de estabilizarse en múltiples formaciones recurrentes y fijas, incluidos algunos planeadores.

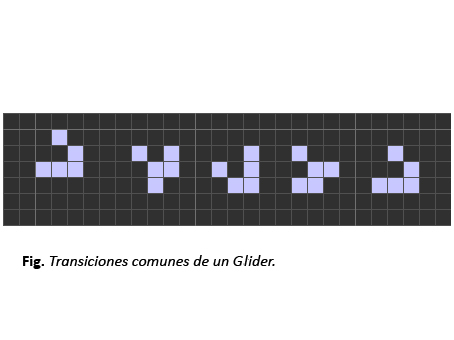
En cuanto a los planeadores o patrones de movilidad, una de las aportaciones originales de Conway fue el descubrimiento de la estructura de cinco células vivas llamada Glider, que resulta encajar en el papel de planeador realizando un viaje en diagonal por la cuadricula. Las transiciones se ven representadas en la siguiente figura:

Ampliamente estudiados por Carter Bays, los automatas celulares de tres dimensiones se enfocan principalmente para encontrar una regla de evolución en tres dimensiones que sea la sucesora del Juego de la Vida en el espacio tridimensional, muchos de sus resultados son de tipo cuantitativo, basados principalmente en la simulación de varias reglas de evolución en pequeños espacios tridimensionales para encontrar estructuras que sean similares al Juego.La aplicación de estos autómatas celulares se centra en el estudio en campos estadísticos.

Son automatas celulares que se desarrollan en un ámbito de ℤ x ℤ x ℤ, que usan el principio de vecindad de Moore a nivel tridimensional. Esto implica que la función de transición ha de tener en cuenta el estado de veintiseis células vecinas además del estado de la célula en cuestión.

Los automatas celulares tridimensionales pueden seguir los mismos principios que los anteriores, aunque dado el incremento de la complejidad de los calculos y el procesamiento, su puesta en práctica no es simple. Sin embargo, y puesto que se pueden considerar automatas celulares tridimensionales con las mismas variables de tipo frontera en el ámbito teórico, se debe considerar que la representacion de los automatas celulares tridimensionales considerando una frontera periódica es en forma de toroide.

Los patrones evolutivos en tres dimensiones son considerados distintos, de forma que se catalogan en complejos, caóticos o triviales.

Las aplicaciones realizadas con los automatas celulares a día de hoy son tan amplias que abarcan profesiones tan dispares como psicología e informática.

Hoy en día se puede concretar el uso de los automatas celulares como método de control estadístico para encontrar patrones aparentemente no triviales en espacios de evoluciones a gran escala, o como elemento de nueva introducción en ámbitos como la arquitectura o la química.

En realidad, podemos generalizar las aplicaciones de los automatas celulares en tres ideas fundamentales: simulación de sistemas naturales, estudios teóricos y realización de tareas específicas.

En el primero, simulación de sistemas naturales, podemos nombrar áreas de la psicología (estudio de comportamiento de masas), medicina (patrones de pigmentación de la piel), ingenieria (mecánica de fluidos), química (modelos de reacciones químicas) o geología y ciencias de materiales (estudio de crecimiento de cristales). Incluso se contempla su uso en la resolución de incendios y su propagación.En segundo lugar, los estudios teóricos se extienden desde el estudio de los sitemas caóticos a la computación en paralelo, la computación universal o el estudio de patrones fractales. Por último, en cuando a la realización de tareas específicas, que se pueden extender desde finalidades artísticas a procesamiento de imágenes y encriptación de datos.Actualmente, ciertas líneas de investigación se centran en la creación de modelos paralelos de sistemas físicos y el procesamiento de datos en paralelo optimizada, mediante automatas celulares.

vi Life 1.0a

viLife es una aplicación creada especificamente durante el desarrollo de este estudio sobre los autómatas celulares, para cubrir la amplia temática de estos en relación a su implementación y estudio visual de sus evoluciones y patrones. Actualmente, el desarrollo atraviesa una fase alfa, en la que llevamos a cabo una pequeña limpieza del código y funcionamiento.

Código fuente

main.cpp

Es el fichero del programa principal que se encarga de evaluar los parámetros y crea la aplicación gráfica.

window.cpp y window.h

Estos dos ficheros corresponden a la clase Window que es la encargada de manejar los eventos que se producen tras la interacción del usuario con la aplicación.

GlWidget.cpp y GlWidget.h

En la clase GlWidget se han implementado todos los métodos necesarios para hacer funcionar la aplicación gráfica de El Juego de la Vida. Nos detendremos en este apartado, pues es el que incluye el algoritmo que hace funcionar el juego de la vida.
En concreto, nos pararemos en la función cuya cabecera es “void evolucionar(unsigned int veces = 1);”.

void GLWidget::evolucionar(unsigned int n)
{
	for (unsigned int veces=0; veces 3))) matriz2[i][j] = MUERTO;
				else if ((matriz[i][j] == VIVO) && ((vivos == 2) || (vivos == 3))) matriz2[i][j] = VIVO;
				else matriz2[i][j] = MUERTO;
				vivos = 0;
			}
		}
		unsigned char **aux;
		aux = matriz;
		matriz = matriz2;
		matriz2 = aux;
		nevoluciones++;
	}
	updateGL();
}

Como podemos apreciar si nos fijamos en este código (en lenguaje C++), la función evolucionar consiste en el anidamiento de cuatro bucles:

• El primero no tiene mayor importancia, puesto que está dedicado a hacer que el autómata evolucione tantas veces como se le indique meidante el parámetro n. Se podría eliminar el bucle y llamar a la función evolucionar tantas veces como queramos que evolucione obteniendo el mismo efecto pero por motivos de implementación se ha decidido hacerlo así.
• El segundo y el tercer bucle recorren la matriz de células para ir comprobando una a una.
• El cuarto bucle nos servirá para comprobar cada uno de los vecinos de la célula que indica la posición determinada por los bucles anteriores. Por ejemplo, si en un determinado momento estamos evaluando la vecindad de la célula situada en la posición (i,j) tendrémos que evaluar sus 8 células vecinas para determinar el estado siguiente de la célula actual. Este bucle nos servirá por tanto para recorrer cada una de esas 8 células cuyas posiciones relativas a (i,j) vienen determinadas por los valores introducidos en el array de vecinos.

A partir de aquí, y en la parte interna de los cuatro bucles, se realizan una serie de evaluaciones de los estados de las células vecinas que son justamente las reglas del juego de la vida.

El resto son detalles de implementación cuya explicación no es objetivo de este texto.

Estado.cpp y Estado.h

Esta clase se ocupa de abstraer un estado y el color con el que se representará en pantalla dicho estado. Se ha creado así para que sea sumamente fácil añadir más posibles estados a una célula.

Funcionamiento de la aplicación

Especificación del tamaño del autómata.

Por defecto, al ejecutar la aplicación se representa un autómata de 100x100 células. Sin embargo, nosotros podemos decidir el tamaño que tendrá nuestro autómata cuando ejecutamos la aplicación. Para ello pasaremos como parámetro en la llamada a la aplicación el tamaño de la matriz que se utilizará para representar el autómata. Basta con ejecutar la aplicación con el siguiente comando:

$ Life.exe -t x

El valor de x será el tamaño que deseamos dar al autómata. En la siguiente imagen vemos como se ha ejecutado la aplicación con un tamaño de 200x200 células.

Observaciones

Para simplificar se ha considerado que el autómata tendrá la misma cantidad de células en ambas direcciones por lo que no se podrá ejecutar un autómata de diferente tamaño en ambos ejes.

Otro apunte a considerar es que hemos utilizado una frontera periódica. Esto significa que la transición de una célula en cualquiera de los extremos depende del estado de la célula opuesta.

Zoom

De las barras situadas a la derecha de la animación, la segunda barra es la encargada de permitir realizar una ampliación de nuestro autómata. Mediante esta acción apreciaremos con más detalle la evolución del autómata en determinadas áreas.

En la siguiente imagen podemos apreciar el zoom a nivel por defecto, que es la mínima ampliación posible.

En cambio, ahora vemos a mayor tamaño una determinada parte del autómata, en este caso el centro del mismo.

Desplazamiento

Mediante esta función podremos desplazarnos hacia otro lugar del autómata cuando hayamos realizado un zoom adicional. Las barras de desplazamiento que hay justo a la derecha y debajo de la animación son las que llevan a cabo este desplazamiento.

Podemos ver un ejemplo en la siguiente imagen, en la cual hemos realizado una ligera ampliación mediante la funcionalidad de zoom y adicionalmente nos hemos desplazado a la esquina inferior derecha del autómata.

En la siguiente ilustración vemos cómo manteniendo el mismo desplazamiento en ambas direcciones hemos aumentado el nivel de zoom obteniendo un mayor detalle en el área que se muestra.

Velocidad

La velocidad de las transiciones (o evoluciones) se controlan mediante la tercera barra de desplazamiento a la derecha de la animación. En un principio esta barra aparece en su posición más alta lo que equivale a una velocidad baja (una transición por segundo). Si desplazamos la barra hasta su posición más baja la velocidad será superior, dependiendo del tamaño del autómata y de la velocidad de nuestra máquina.

En la siguiente imagen hemos aumentado al máximo la velocidad con lo cual hemos obtenido un alto número de evoluciones en poco tiempo.

Página principal de la aplicación

Golly 1.2

Al margen de nuestro propio software y relacionado con los automatas celulares, podemos nombrar miles de programas especificos de simulación. Sin embargo, para esta redacción se ha usado Golly 1.2 para entornos Win32, gratuito y disponible para descarga. Además, este software esta desarollado para funcionar tanto en windows como en linux.

• A New Kind of Science, de Stephen Wolfram. ISBN 1579550088
• The Computer – My Life, de Konrad Zuse. ISBN 0387564535
• The Theory of Self-reproducing Automata, John Von Neumann. ISBN 9780598377982
• Theory and Application of Cellular Automata, Stephen Wolfram. ISBN 9971501236
• Mathematical Games: The fantastic combinations of John Conway's new solitaire game "Life", Martin Gardner . Revista “Scientific American”.
• Rechnender Raum, Elektronische Datenverarbeitung, vol. 8, pages 336-344, Konrad Zuse , 1967.
• Three Scientists and Their Gods, Robert Wright, 1989. ISBN 0-06-097257-2
• Chaos theory, de Gregory Rae.